Avançando no quesito Temporal através da Persistência Parcial

Publicado em 26 de mar. de 2024

No post Introdução a Estruturas de Dados Efêmeras e Persistentes pude abordar sucintamente a diferença conceitual entre Estruturas Efêmeras e Estruturas Persistentes. Tópico também abordado foi a existência de 4 formas diferentes de Persistência. Nesse post, venho falar com mais detalhes a respeito da Persistência Parcial.

Persistência Parcial

Vale a pena relembrar que nesse nível de persistência podemos consultar qualquer versão de uma estrutura, porém atualizações só podem ser realizadas na última versão.

Neste nível como dito a ideia é implementar de uma maneira de conservar estados anteriores da estrutura, mas apenas para consultas. Sendo assim, como é possível implementar Persistência Parcial de forma eficiente?

Para essa pergunta não existe uma única resposta, ao longo do tempo técnicas foram introduzidas de modo a tornar o processo mais eficiente. Ainda assim vale a pena conhecer os processos adotados no passado.

Para seguir uma linha de raciocínio para cada exemplo vou realizar a seguinte Sequência de Operações:

Iniciar a Estrutura vazia;
Adicionar um valor 1;
Adicionar um valor 2;
Adicionar um valor 3;
Alterar o valor de 2 para 5;
Alterar o valor de 5 para 9;
Adicionar um valor 4;
Remover o valor 3;
Remover o valor 4;
Remover o valor 1;
Remover o valor 9.

Além de descrever os métodos para se atingir a Persistência Parcial, uma referência deve ser estabelecida a fins de comparação. Tomaremos como parâmetro uma Lista Encadeada e de diferentes formas iremos transformá-la em Parcialmente Persistente. Mas, antes de qualquer conversão, vale representar uma Implementação Efêmera.

Não pretendo abordar o código de implementação de cada método neste post. Por fins de simplicidade me limitarei a representar a estrutura apenas utilizando os tipos em código e uma sequência visual da estrutura reagindo as operações propostas.

Exemplo Efêmero

Acredito não ser novidade para ninguém para representar os tipos, deste exemplo, definiremos uma Lista Encadeada através de um Modelo de Máquina de Ponteiros. Podemos pensar num agrupamento linear de nós, denominados Nodes, em que cada nó pode conter dados e ponteiros para outros nós. Podemos definir os tipos da seguinte forma:

struct Node<T> {
  value: T;
  pointer: Option<Box<Node>>;
}

struct EphemeralLinkedList<T> {
  root: Option<Box<Node>>;
}

Tendo definido os tipos, segue a representação visual da Estrutura:

Começar com a Estrutura vazia:
Adicionar um valor 1:
Adicionar um valor 2:
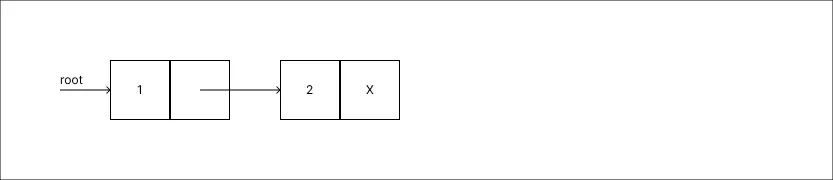
Adicionar um valor 3:
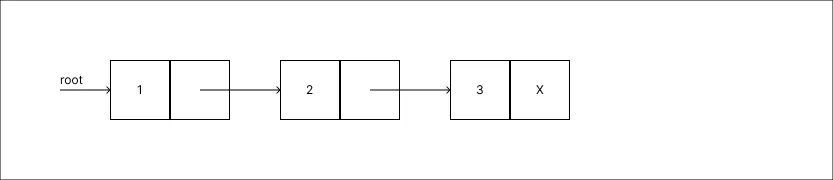
Alterar o valor 2 para 5:
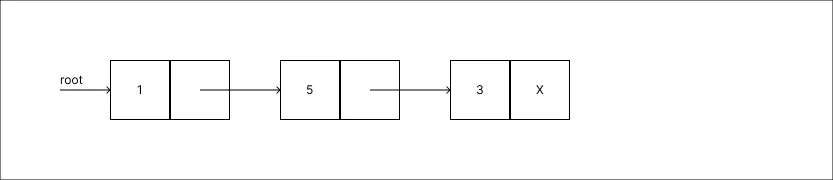Assim que o valor é atualizado a informação a respeito do antigo valor 2 passa a ser irrecuperável.
Alterar o valor 5 para 9:
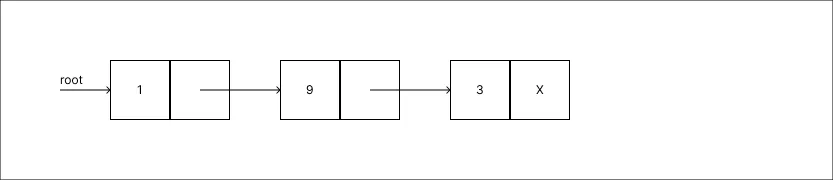Novamente, assim que o valor é atualizado a informação anterior é totalmente perdida.
Adicionar um valor 4:
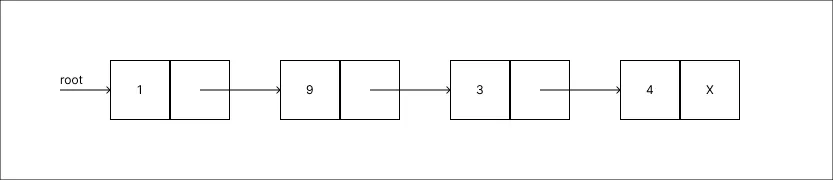
Remover o valor 3:
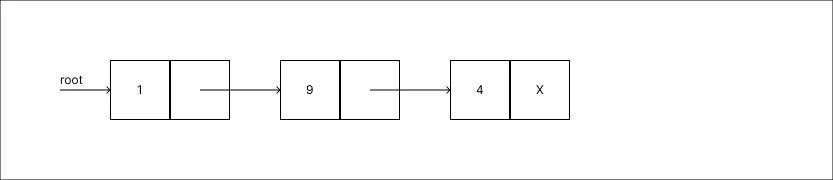Ao remover o Node perde-se a informação que este antes continha.
Remover o valor 4:
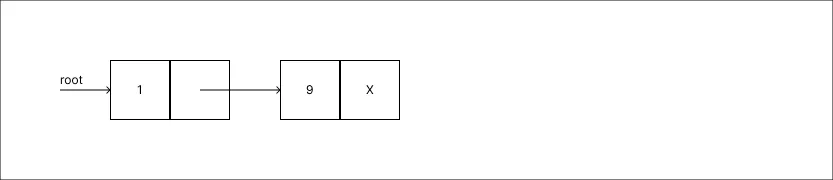
Remover o valor 1:
Remover o valor 9:

A medida que alterações são realizadas a informação prévia é perdida. De modo que, ao final do processo, após uma operação de remoção para cada operação de inserção a Estrutura de Dados não contém registro algum do passado.

Obviamente na maioria dos casos, esta será a melhor implementação possível, visto que nem todo contexto se beneficia da conservação dos estados anteriores. Uma vez que para manter toda e qualquer informação há um custo, seja de maior uso de memória ou de processamento.

Entretanto, caso a perda de informação toque negativamente um processo, a utilização de uma implementação Efêmera, como este exemplo, trará inúmeras dificuldades. Sendo assim, vamos para o primeiro método abordado neste post.

Método das Cópias

O método mais primitivo possível para implementar a Persistência Parcial, consiste em gerar cópias da estrutura para cada alteração realizada e manter uma lista de versões que disponibilize consultas para toda e qualquer versão desejada.

Neste método a estrutura dos Nodes utilizados não sofrerá alterações, em comparação com Modelo Efêmero, permanecendo como:

struct Node<T> {
  value: T;
  pointer: Option<Box<Node>>;
}

Neste método, diferentemente da Estrutura Efêmera, não podemos ter uma root que aponte diretamente para um nó, visto que para cada alteração uma nova cópia da estrutura é armazenada. Para manter acesso de cada cópia individualmente podemos utilizar um Vetor.

use std::colections::HashMap

struct LinkedList<T> {
  root: Option<Box<Node>>
}

struct CopyMethodLinkedList<T> {
  root: Vec<LinkedList<T>>
}

Tendo definido os tipos, segue a representação visual da Estrutura:

Começar com a Estrutura vazia:
Perceba que a raiz não começa literalmente vazia, como a raiz neste cenário constitui-se de um Vetor de versões, esta então deve começar com um item correspondente a versão inicial da estrutura. Um Vetor vazio pode expressar que a estrutura nunca esteve vazia, por isso principalmente deve ser iniciada com uma versão sem nós.
Adicionar um valor 1:
Ao realizar uma operação a raiz anterior não é alterada uma nova é adicionada, com as mudanças processadas.
Adicionar um valor 2:
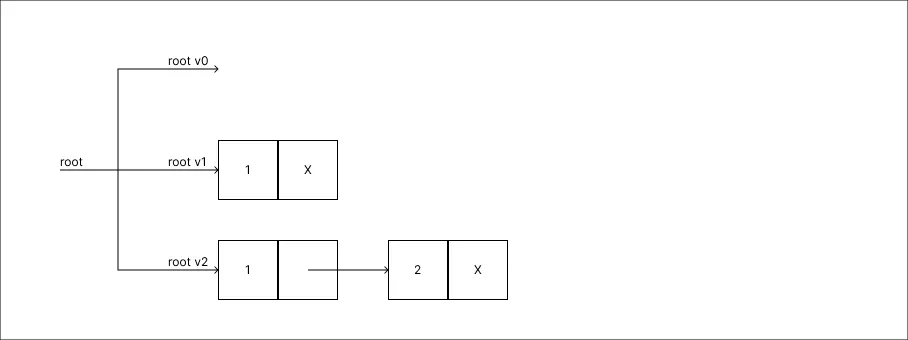
Adicionar um valor 3:
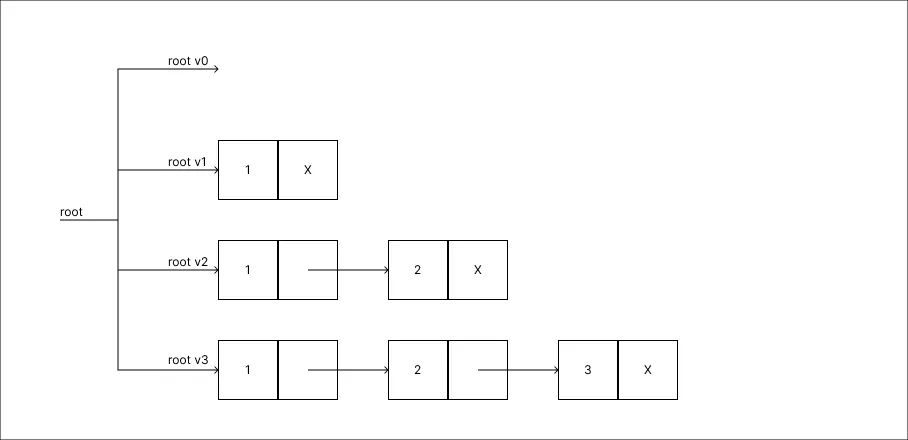
Alterar o valor 2 para 5:
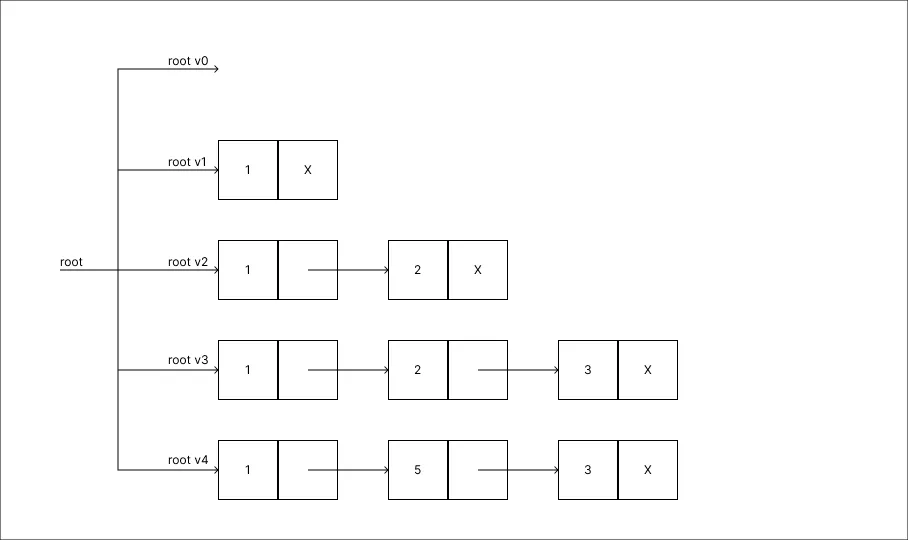
Alterar o valor 5 para 9:
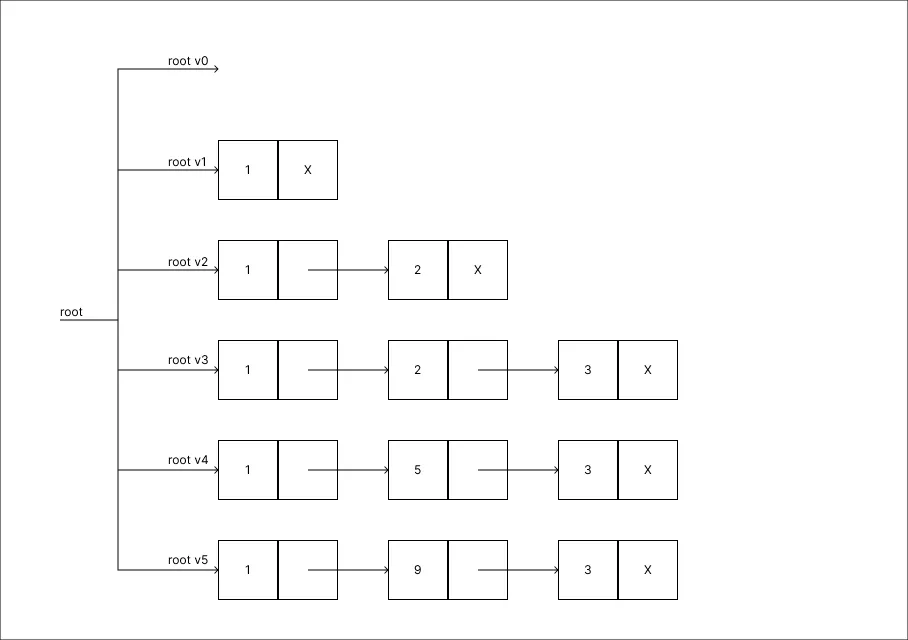
Adicionar um valor 4:
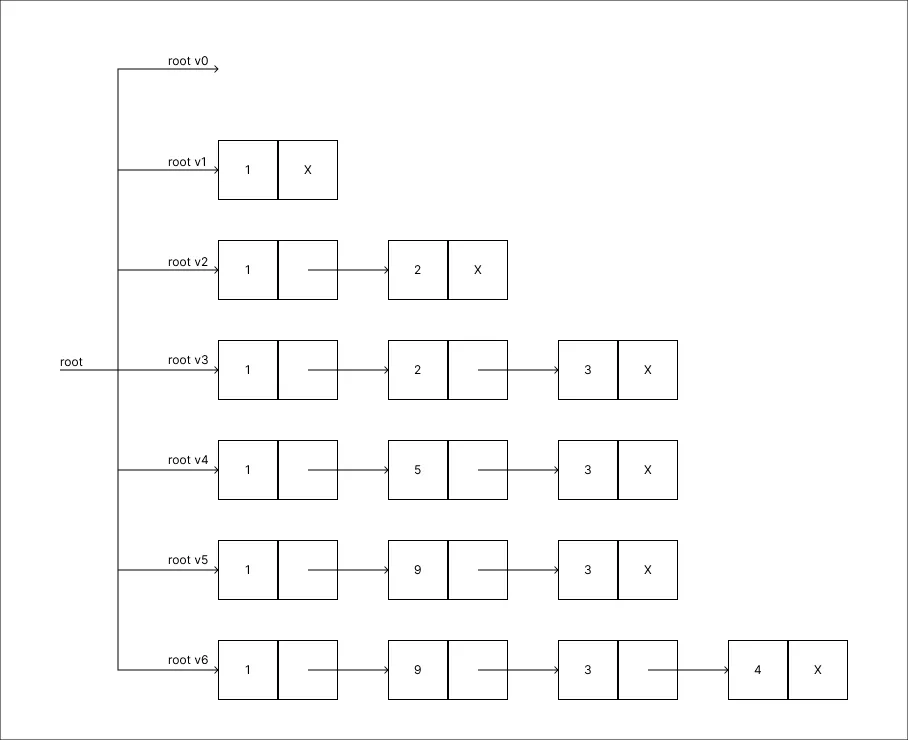
Remover o valor 3:
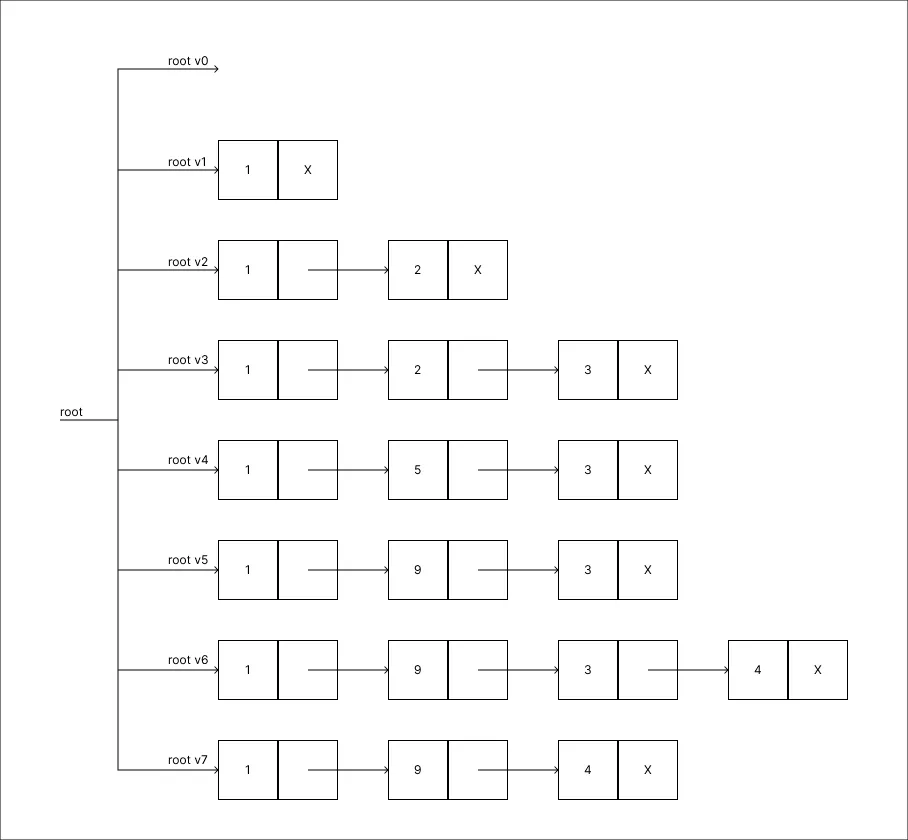
Remover o valor 4:
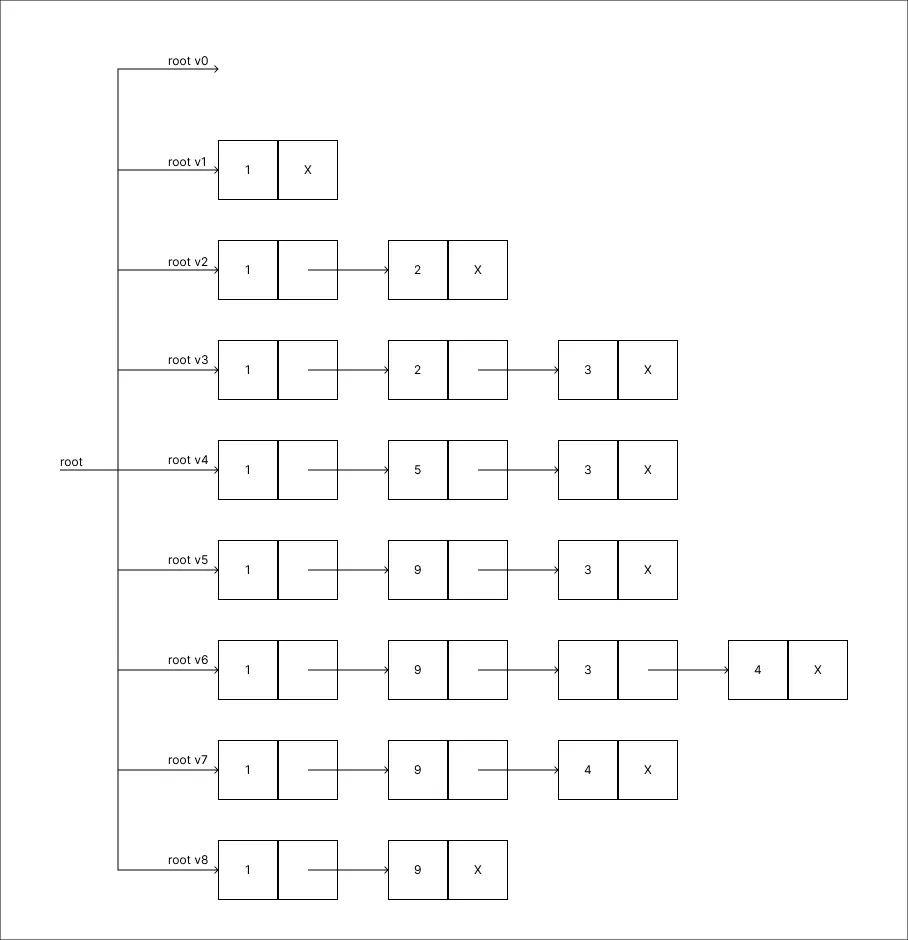
Remover o valor 1:
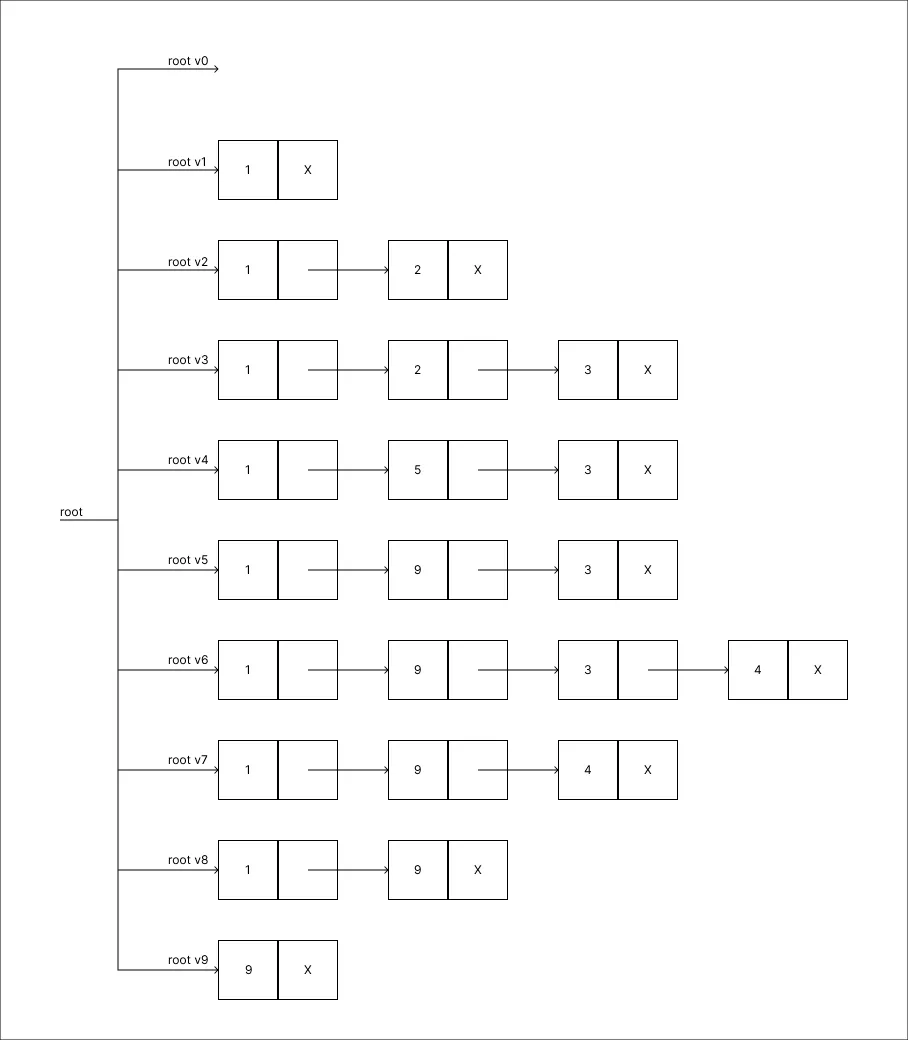
Remover o valor 9:

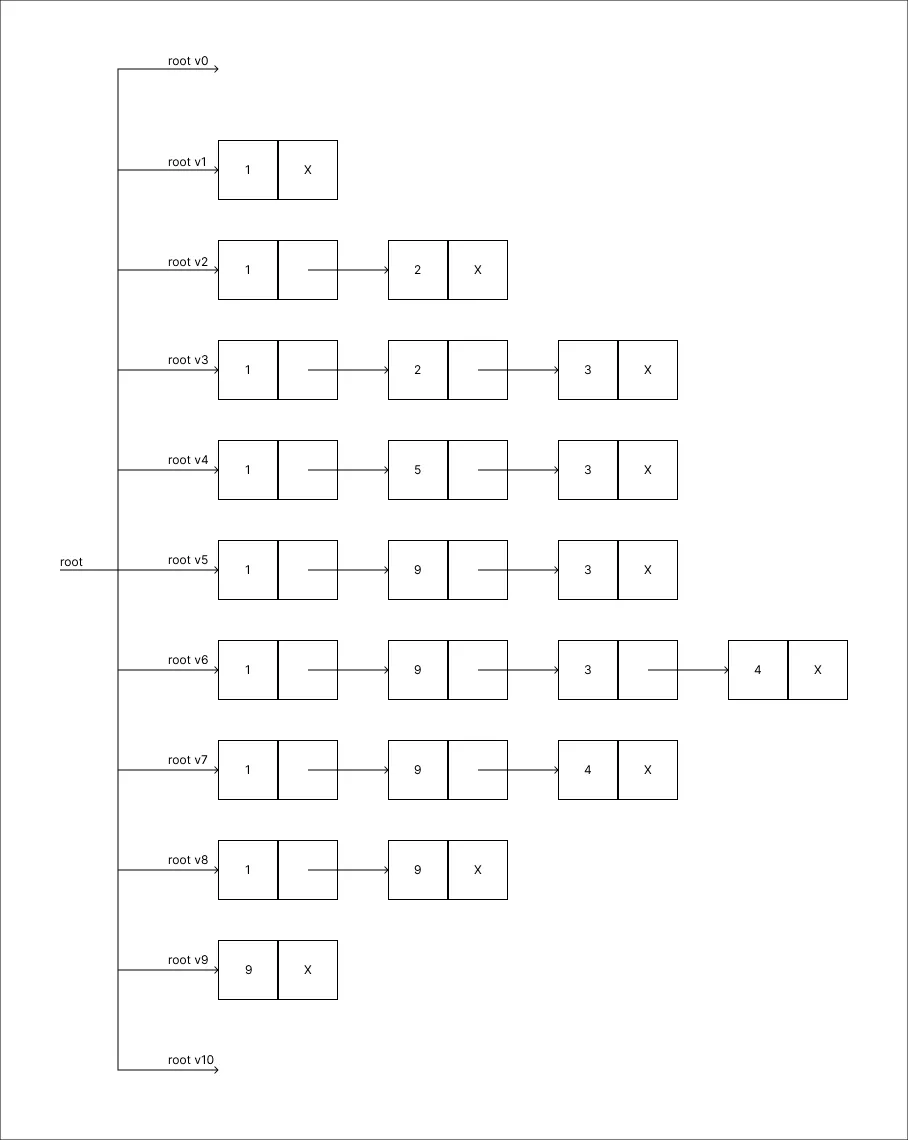
Nesta estrutura, toda e qualquer versão existente está disponível para consulta e para satisfazer a Persistência Parcial basta então restringir atualizações a última versão. Tendo isto sido feito esta implementação pode ser tida como Parcialmente Persistente.

Note que ao decorrer do processo cada atualização adiciona a estrutura uma versão equivalente a versão efêmera anteriormente apresentada para tal atualização.

Como este método utiliza-se de cópias para conservar a informação. A medida que a Estrutura cresce em números de Nodes, a atualização realizada passa a ser cada vez menos significante comparada a quantidade de memória despendida para realizar a cópia de todo o resto da estrutura que não será modificado.

Ainda que a estrutura não venha a atingir uma quantidade exagerada de Nodes, o consumo de memória tende apenas a crescer mais e mais, logicamente, em quantidades proporcionais ao tamanho das versões.

Ao longo da história outros métodos foram propostos para lidar com essa questão. É hora de abordar outro dos primeiros métodos. Segue o método do Histórico.

Método do Histórico

Como dito no nome o método em questão utiliza de um histórico para manter o controle de versões da Estrutura. Este histórico funcionará com um registro ordenado das alterações realizadas, sendo assim, suprimindo a exigência de manter em memória qualquer versão.

No que tange as atualizações, para realizar quaisquer alterações na estrutura basta apenas inserir no Array o registro, note que no parágrafo passado delimitamos que este registro deve ser ordenado, tendo em consideração que para Persistência Parcial não desejamos que atualizações possam ser realizadas a partir de qualquer versão devemos delimitar que toda e qualquer atualização deve ser inserida na última posição.

Quanto as consultas, para realizar qualquer consulta devemos processar a estrutura para a versão desejada e só então realizar a consulta.

Para representar tal solução não há necessidades de Nodes ou alguma Estrutura com uma root, apenas um tipo que defina as operações e uma estrutura que armazene esse tipo de forma sequencial, como um Vetor. Tal qual pode ser representado da seguinte maneira:

enum Op {
  Add,
  Remove
}

enum Update<T> {
  ValueUpdate { from: T, to: T },
  NodeUpdate { value: T, op: Op }
}

struct HistoryMethodLinkedList<T> {
  history: Vec<Update<T>>
}

Tendo definido os tipos, segue a representação visual da Estrutura:

Começar com a Estrutura vazia:
Ao contrário dos exemplos anteriores, que a Estrutura da versão vazia se tratava de uma root que não apontava para um Node. Neste caso não apenas não temos uma root tampouco uma estrutura concreta.
Adicionar um valor 1:
Ao realizar a atualização apenas inserimos no Vetor o registro que descreva a mudança.
Adicionar um valor 2:
Adicionar um valor 3:
Alterar o valor 2 para 5:
Alterar o valor 5 para 9:
Adicionar um valor 4:
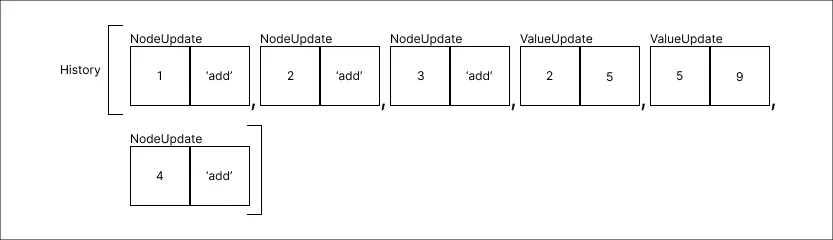
Remover o valor 3:
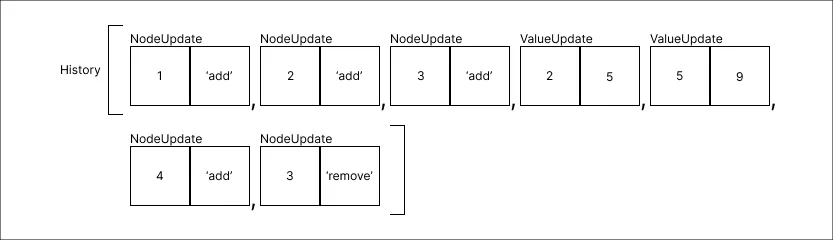
Remover o valor 4:
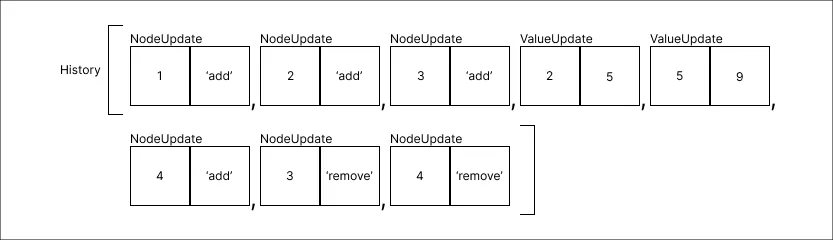
Remover o valor 1:
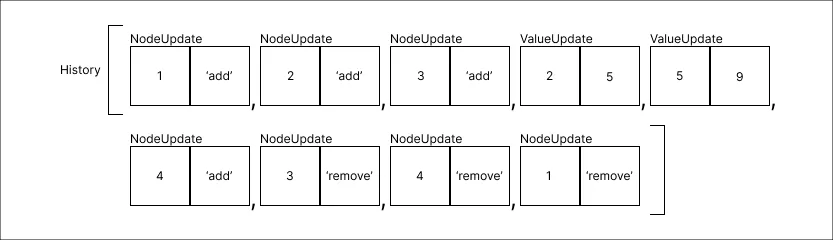
Remover o valor 9:

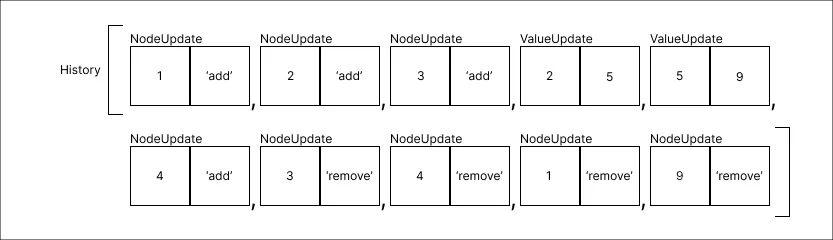
Através do registro das alterações conseguimos satisfazer as condições necessárias para atingir a Persistência Parcial, novamente vale reiterar que para manter a condição satisfeita novos registros devem sempre ser inseridos ao fim do histórico.

Divergentemente do método das cópias o uso de memória nesta solução é baixo e não escala com o crescimento da estrutura. Além do custo de memória reduzido processar novas operações tem o custo de inserção em um Vetor.

O calcanhar de Aquiles dessa abordagem são as consultas, realizar uma consulta exige montar a estrutura do zero o que será caro em termos processamento, principalmente consultando versões distantes do início. Parte expressiva desse problema está no fato de que para cada consulta a estrutura deve ser montada novamente, a falta de aproveitamento de montagens anteriores torna o processo muito ineficiente.

Porém atribuir uma solução de cache, memorização ou qualquer técnica dinâmica semelhante não é muito interessante, num cenário mediano na tentativa de reduzir o problema das consultas bateríamos novamente na tecla na memória. Podendo até a manter em registro um histórico completo de todas as versões assim como no método das cópias, e em adicional o histórico de alterações.

Apesar da baixa utilização de memória desta proposta a uma compensação suficientemente negativa no custo de processamento de cada consulta. Por razões como esta, abordaremos um outro método, o método Híbrido de Histórico.

Método Híbrido

Trata-se de um meio termo entre o Método do Histórico e o Método das Cópias. Assim como no Método do Histórico este método utilizará de uma lista para manter o registro de alterações. Também compartilhando semelhanças com o Método das Cópias, este apresenta uma raiz com ramificações que apontam para diferentes versões.

No método anterior debatemos a ideia de utilizar alguma técnica dinâmica para recuperar a construção de versões e agilizar as consultas. O problema comentado foi de que sem um devido controle, versões demais poderiam ser armazenadas e novamente haver problemas quanto a otimização do uso de memória.

A abordagem gira em tordo desse controle. Este método estabelece um número fixo N de atualizações para cada versão da estrutura construída. Sendo assim, cada ramificação nesta solução irá conter uma estrutura construída e uma lista que pode chegar até a N atualizações.

Para cada N novas atualizações uma nova ramificação é construída, permitindo manter uma disponível a informação de toda e qualquer atualização realizada. Podemos definir os tipos da seguinte forma:

enum Op {
  Add,
  Remove
}

enum Update<T> {
  ValueUpdate { from: T, to: T },
  NodeUpdate { value: T, op: Op }
}

struct Node<T> {
  value: T;
  pointer: Option<Box<Node>>;
}

struct Step<T, const N: usize> {
  structure: LinkedList<T>,
  updates: [Update<T>, N]
}

struct HybridMethodLinkedList<T, const N: usize> {
  steps: Vec<Step<T, N>>
}

Tendo definido os tipos, segue a representação visual da Estrutura:

Começar com a Estrutura vazia:
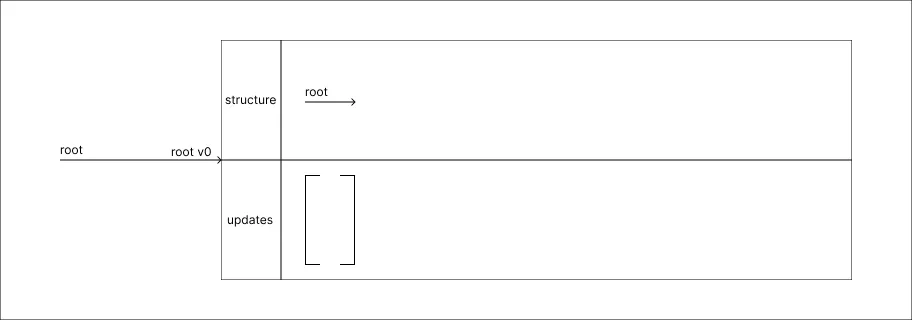Novamente temos a presença de uma root, porém, ao contrário do Modelo das Cópias a root não aponta diretamente para um Node. Neste caso instância vazia contém uma ramificação para versão zero, nessa ramificação há uma estrutura vazia construída e uma lista de atualizações também vazia.
Adicionar um valor 1:
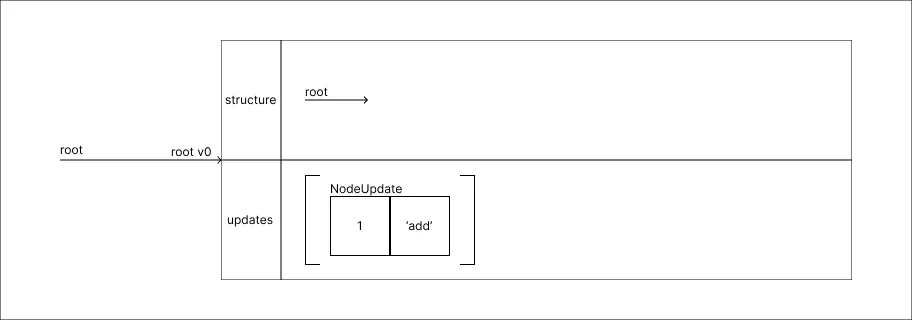A medida que atualizações são realizadas, faz-se a adição da atualização na lista de updates, enquanto a structure permanece inalterada.
Adicionar um valor 2:
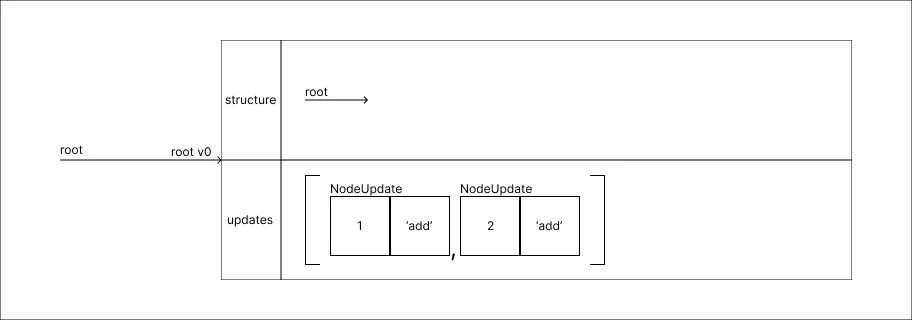
Adicionar um valor 3:
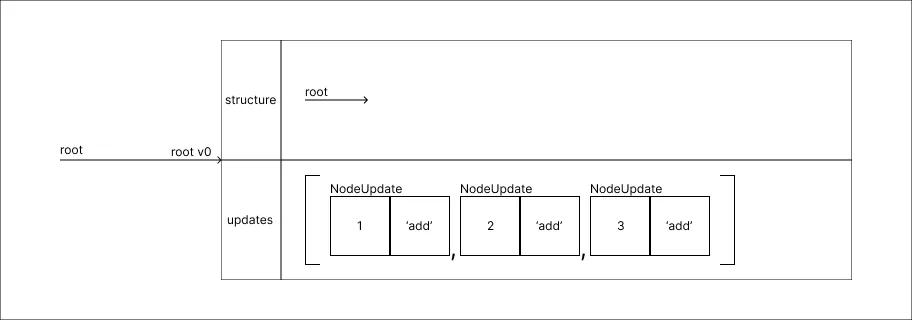
Alterar o valor 2 para 5:
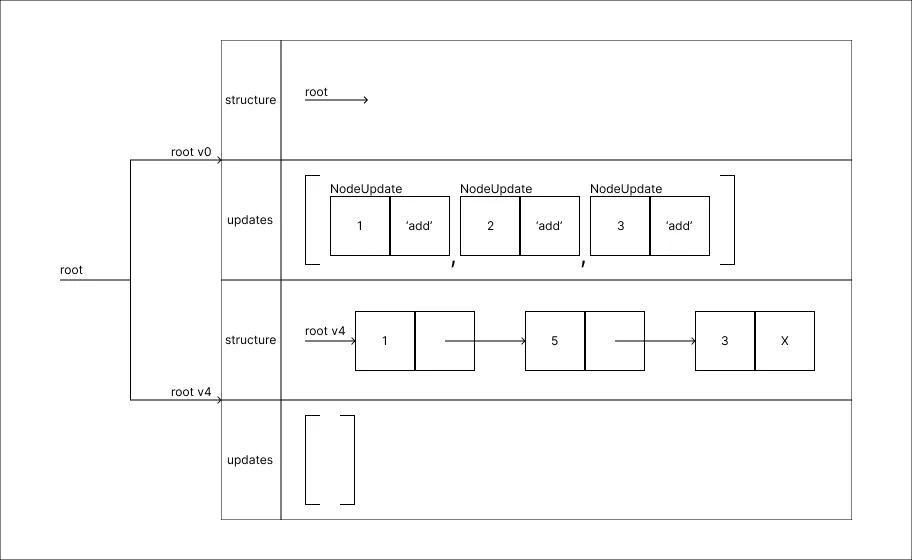Atingindo o valor N de atualizações que cada ramificação deve suportar, uma nova ramificação é criada, nesta etapa ocorre o processamento de uma structure com as atualizações realizadas até então.
Alterar o valor 5 para 9:
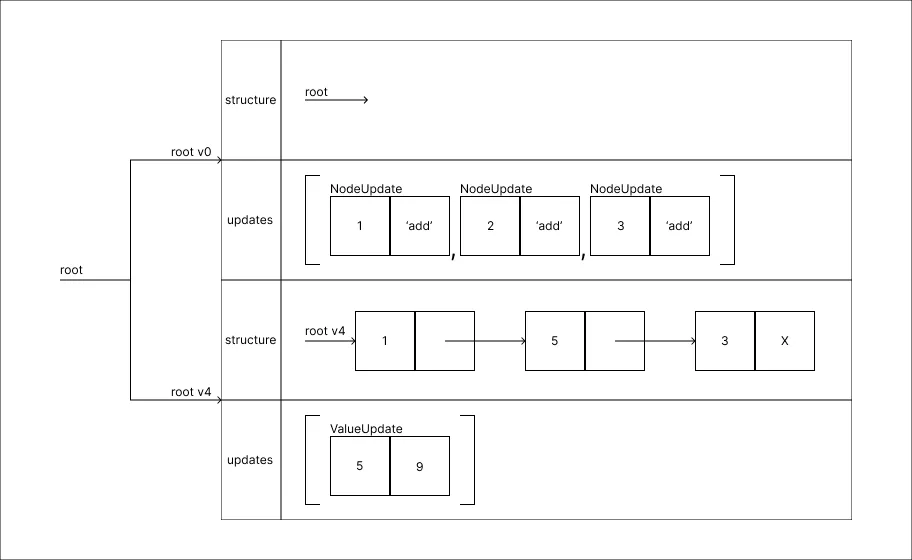
Adicionar um valor 4:
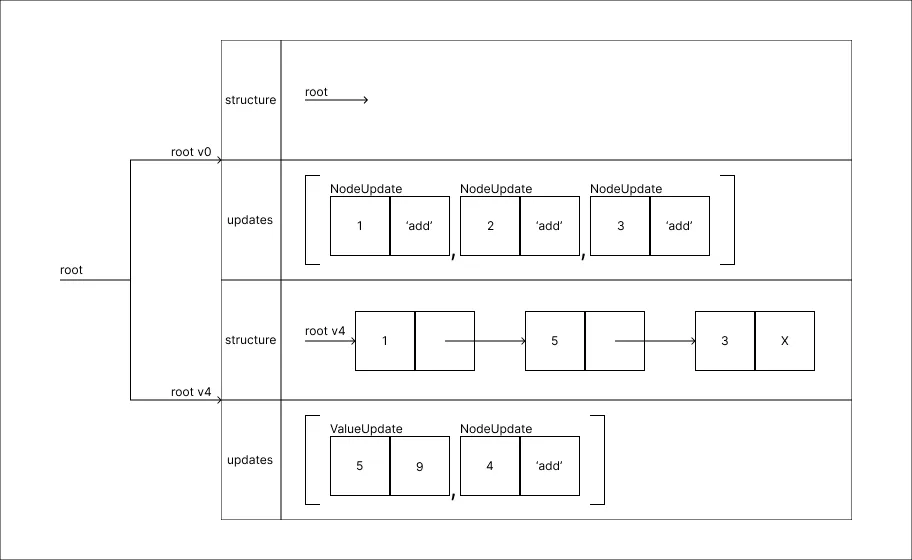
Remover o valor 3:
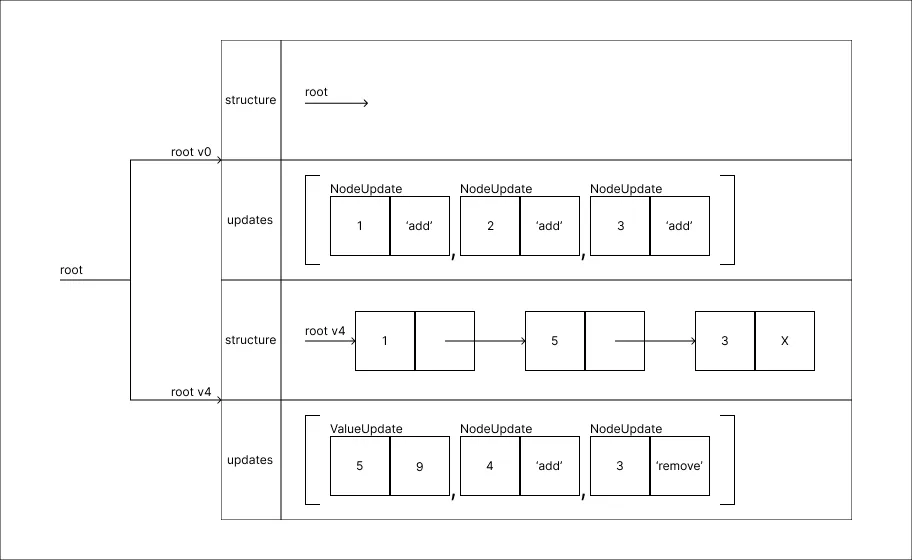Assim como nos métodos anteriores para implementação da Persistência Parcial, perceba-que, ainda que uma operação de remoção seja processada informações não são perdidas.
Remover o valor 4:
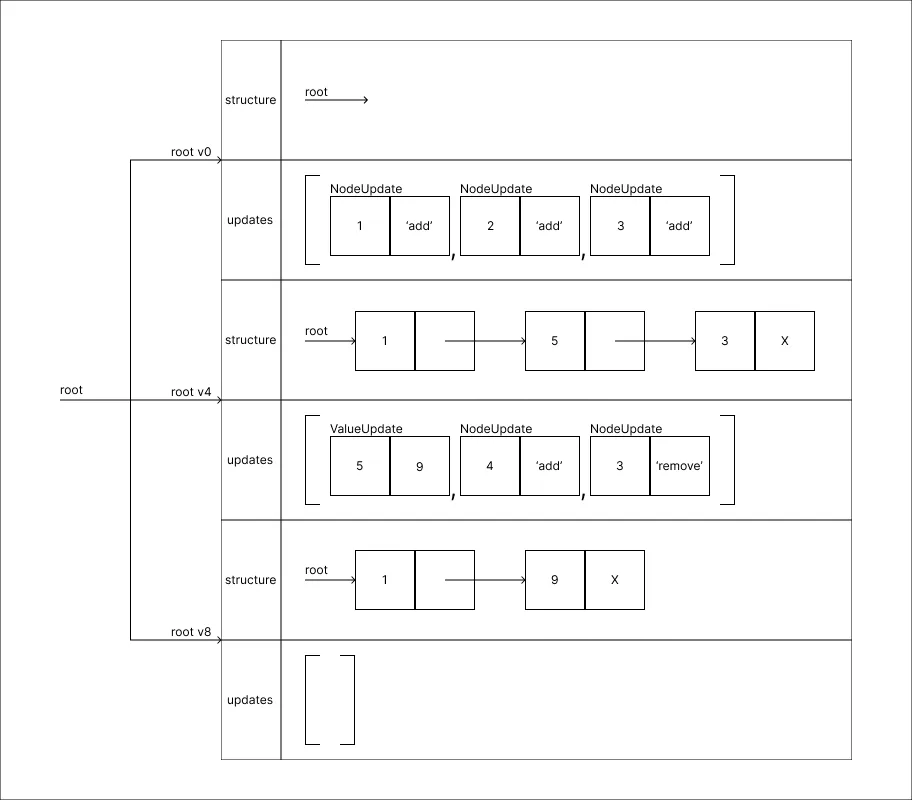
Remover o valor 1:
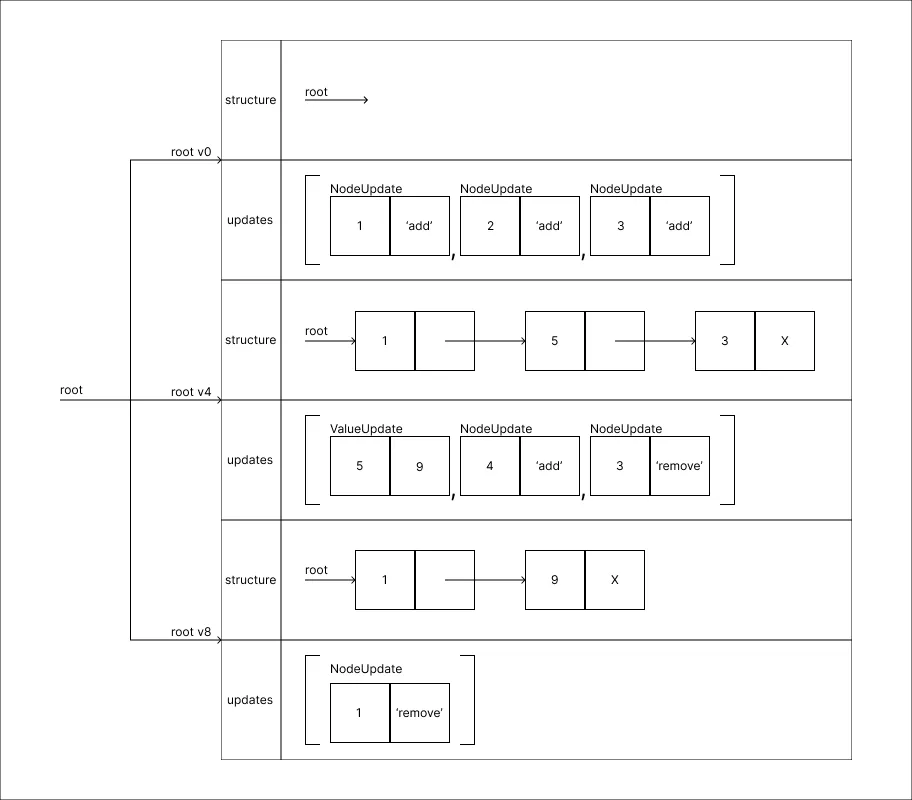
Remover o valor 9:

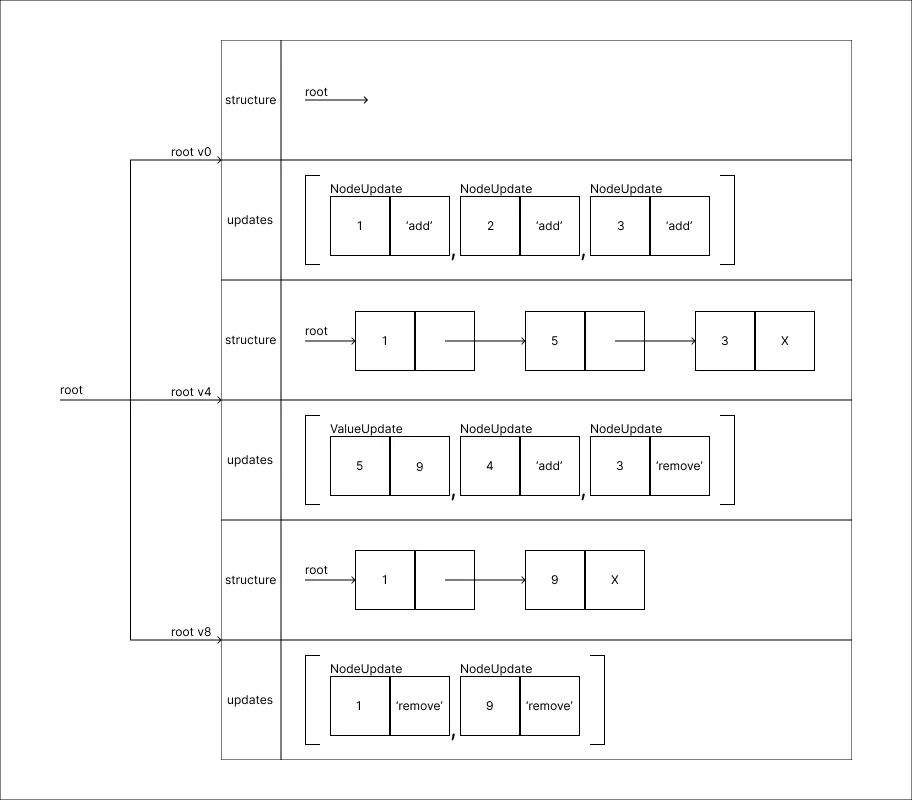
A solução em questão faz um balanço entre os custos de memória para armazenar as diversas cópias do Método das Cópias e o custo de processamento das consultas do Método do Histórico, como diz o nome trata-se de uma solução híbrida.

Note que há um detalhe flexível nesta implementação. No quinto passo, ao alterar o valor de 2 para 5, uma nova ramificação é criada e a estrutura dessa ramificação já contém a mudança processada. Uma outra forma de fazer essa implementação seria por construir apenas a versão anterior e inserir a atualização no registro. Porém nessa outra abordagem, a estrutura armazenada seria equivalente a N - 1, logo o que no exemplo é v4 nessa abordagem seria v3.

Perto dos outros métodos para conversão em Parcialmente Persistente este utiliza menos memória e tem um custo de consulta amortizado. Mas ainda assim, perto de uma estrutura Efêmera, custa caro.

E esse custo pode ser atribuído aos processos realizados para manter a informação. Perceba que todos os métodos utilizam de clones dos Nodes (para o método do Histórico os Nodes são constantemente clonados a cada consulta). Nodes são pouco aproveitados no processo. Deste ponto trata o próximo método.

Um Método Mais Eficiente

Os métodos anteriores, ainda que tenham cumprido com o objetivo de implementar a Persistência Parcial, falham no que tange a eficiência. Utilizam de muitos recursos, para satisfazer as condições desejadas.

Um método mais eficiente é também mais simples. O próximo método a ser abortado é denominado de Fat Node, e como o nome indica a ideia é permitir que as alterações sejam realizadas e armazenadas no próprio Node, fazendo com que este cresça em tamanho.

Para permitir tais adequações de modo eficiente algumas modificações têm de ser realizadas a estrutura do Node. O Node segue mantendo um campo para valor e para ponteiro. E além destes, passará a conter um campo para uma lista de modificações e um campo para a versão em que o Node foi adicionado.

A depender das operações realizadas com a estrutura a root pode apontar para diferentes nós, como por exemplo no caso de exclusão do primeiro nó. Neste caso para a root utilizaremos de um HashMap para designar cada ramificação de acordo com as versões, pois nem toda versão terá uma ramificação e uma nova versão pode ou não ser gerada a depender da exclusão da atual root.

struct Mod<T> {
  label: String;
  version: String;
  value: T;
}

struct FatNode<T> {
  value: T;
  version: String;
  pointer: Option<Box<FatNode<T>>>;
  mods: Vec<Mod<T | Option<Box<FatNode<T>>>>>
}

struct FatNodeMethodLinkedList<T> {
  root: HashMap<i32, Option<Box<FatNode<T>>>>;
}

Tendo definido os tipos, segue a representação visual da Estrutura:

Começar com a Estrutura vazia:
De forma semelhante ao Método das Cópias temos uma root que é iniciada com um HashMap de versões, já contendo um item correspondente a versão inicial da estrutura.
Adicionar um valor 1:
Diferentemente do Método das Cópias e de forma semelhante ao Método Híbrido, aqui nem toda alteração vai gerar uma nova versão.
Adicionar um valor 2:
Não precisamos adicionar modificador à primeira alteração feita no ponteiro, uma vez que o node subsequente tem o rótulo da versão, sabemos que a apenas a partir dessa versão temos o ponteiro naquela posição.
Adicionar um valor 3:
Alterar o valor 2 para 5:
A atualização é adicionada a lista de modificações.
Alterar o valor 5 para 9:
Adicionar um valor 4:
Remover o valor 3:
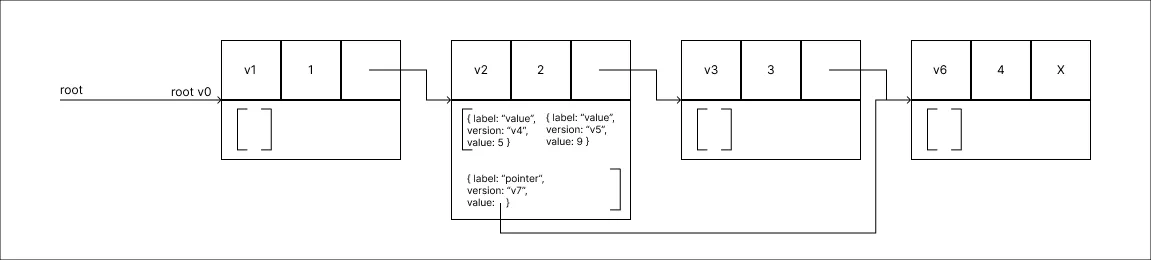Na remoção de um valor, apenas adicionamos uma atualização a lista de modificações, contendo uma alteração ao campo de ponteiro, ponteiro este que passa a aportar para o próximo node na sequência. Perceba que o Node com valor 3, segue na estrutura na mesma posição contendo as mesmas informações.
Remover o valor 4:
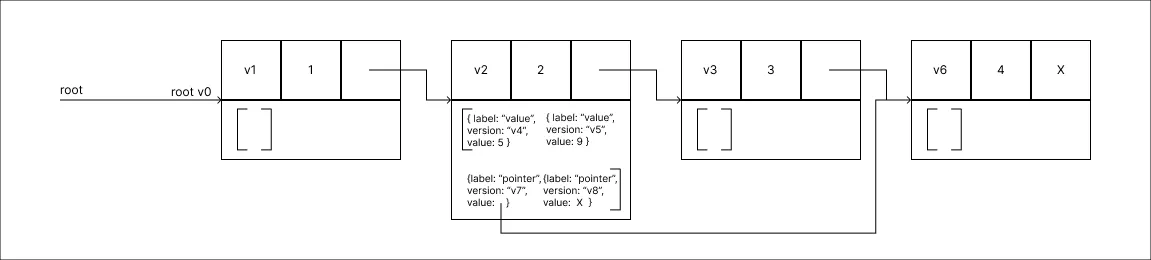Novamente um Node é removido na versão em questão, nesse caso, como não há outro node na sequência do removido a modificação então deve receber o valor respectivo ao caso vazio.
Remover o valor 1:
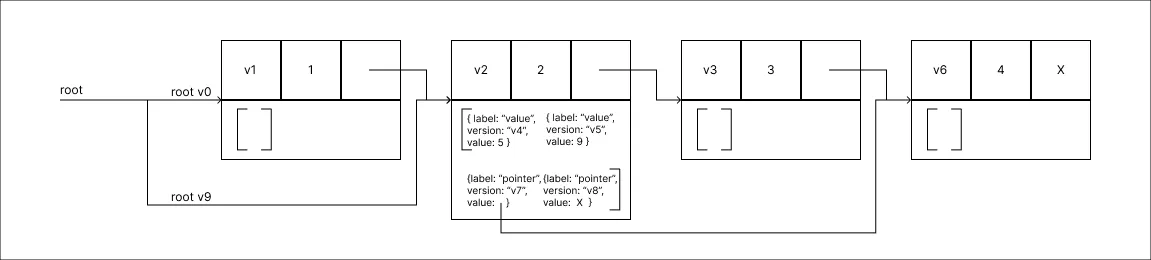A root da versão v0, a mais recente até então, aponta diretamente para o Node que será removido, neste caso ou em casos de inserções na primeira posição, uma nova raiz é adicionada ao HashMap de ramificações.
Remover o valor 9:

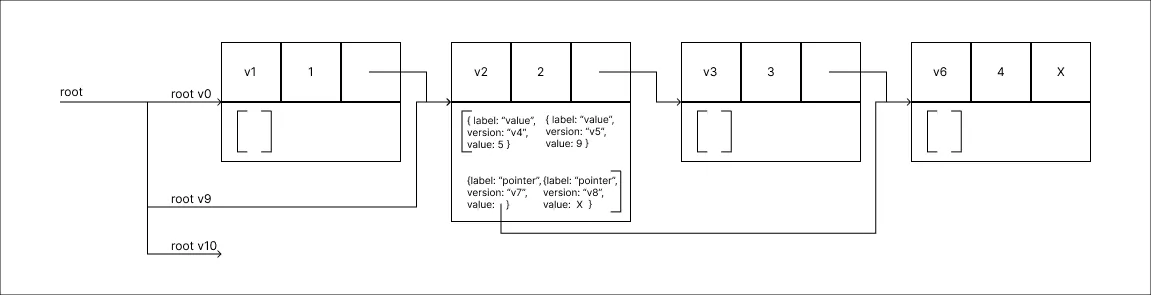
Modelo mais próximo da Estrutura Efêmera até então. Segue estrutura semelhante, mantendo as atualizações no próprio Node e evitando processos de duplicação. Dessa forma reduzindo a quantidade de memória necessária no decorrer do processo.

Um contraponto dessa abordagem é que os Nodes não tem delimitação de crescimento. Uma vez que para realizar qualquer consulta as alterações presentes no campo de modificações devem ser processadas, Nodes altamente modificados podem trazer dificuldades em consultas. De modo semelhante ao que foi abordado no Método do Histórico.

Imagine que um Node com inúmeras atualizações é frequentemente consultado, toda consulta será cara. Sendo assim uma otimização que pode ser feita a esse método, e disso trata o próximo método.

Um Método Ainda Mais Eficiente

Método conhecido como Node Spliting. Essa solução muito se assemelha a solução abordada no Método Híbrido, neste caso definiremos um número arbitrário N de modificações que um Node pode aceitar e caso alguma modificação extra seja realizada, esta deve ser processada em um Node a parte.

No processo de implementação da divisão de um Node há uma dificuldade que é manter atualizada a referência para o Node mais recente. Para que seja possível atualizar quaisquer referências no momento da divisão, adota-se a estratégia de manter um ponteiro inverso, apontando para os Nodes que apontam para o Node que será dividido, dessa forma após a divisão podemos acessar os antecessores e realizar a atualização do ponteiro para o novo Node.

Os tipos podem ser representados da seguinte forma:

struct Mod<T> {
  label: String;
  version: String;
  value: T;
}

struct FatNode<T, const N: usize> {
  value: T;
  version: String;
  pointer: Option<Box<FatNode<T>>>;
  back_pointer: Option<Box<FatNode<T>>>
  mods: [Mod<T | Option<Box<FatNode>>>; N]
}

struct NodeSplittingMethodLinkedList<T, const N: usize> {
  root: HashMap<String, Option<Box<FatNode<T, N>>>>;
}

Tendo definido os tipos, segue a representação visual da Estrutura:

Começar com a Estrutura vazia:
Assim como no Método do FatNode temos uma root que é iniciada com um HashMap de versões, já contendo um item correspondente a versão inicial da estrutura.
Adicionar um valor 1:
Adicionar um valor 2:
Adicionar um valor 3:
Alterar o valor 2 para 5:
Alterar o valor 5 para 9:
Adicionar um valor 4:
Remover o valor 3:
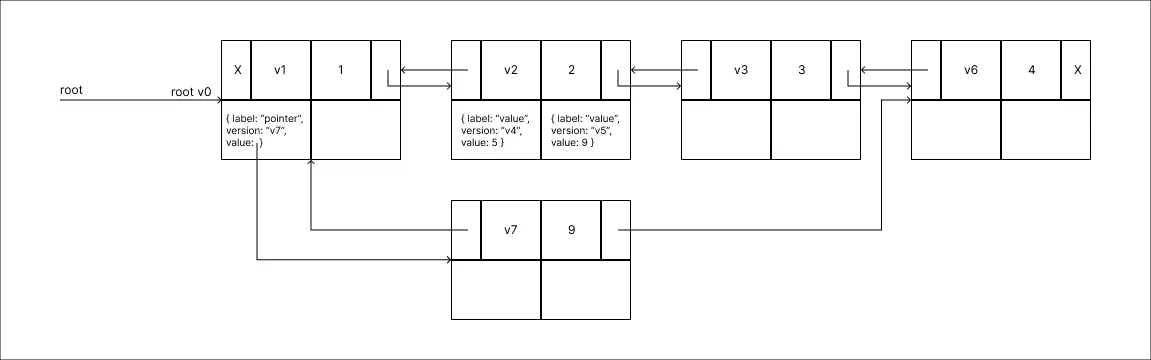Ao passo de remover o valor 3 faz-se necessário adicionar uma modificação ao seu nó antecessor, porém este já se encontra totalmente preenchido. Dessa forma como ilustrado a solução é realizar o Split do Node, e nesse processo uma modificação também deve ser incluída no Node antecessor ao dividido. Além disso, perceba que o novo Node é gerado com os campos mais atualizados e já incluindo a alteração realizada na operação.
Remover o valor 4:
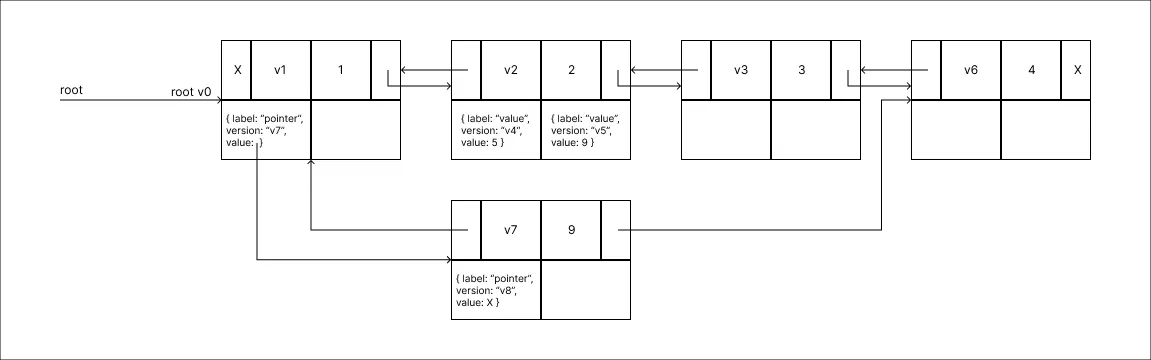
Remover o valor 1:
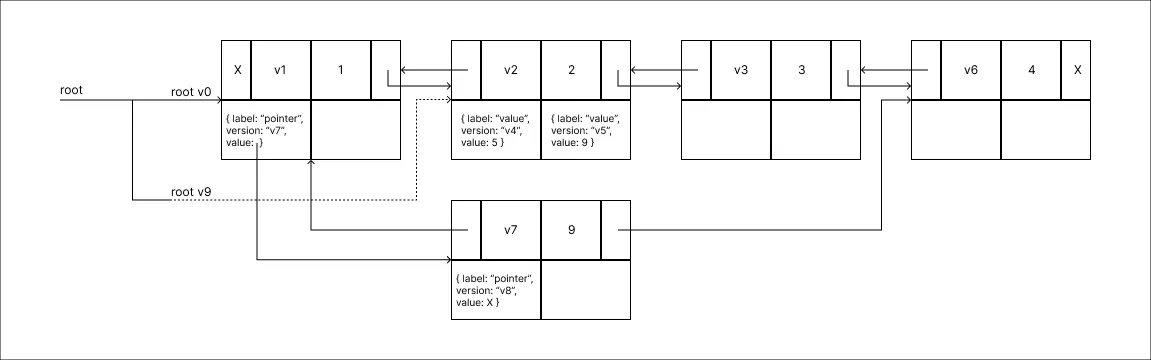
Remover o valor 9:

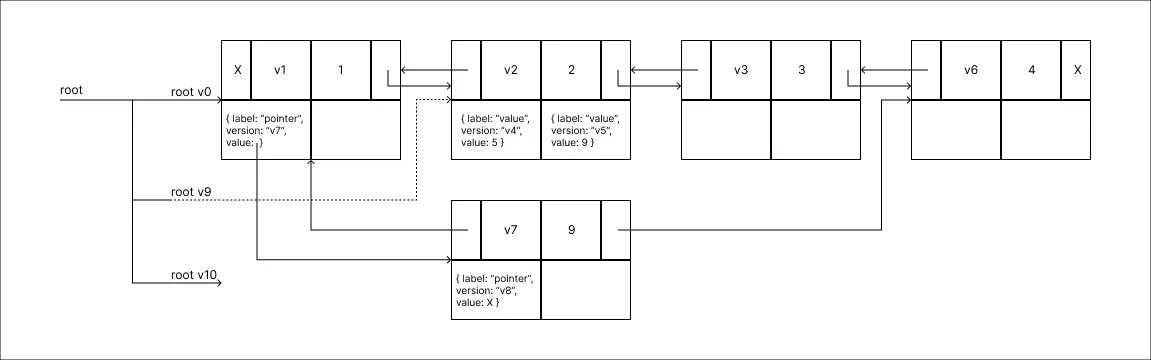
Não muito diferente do resultado obtido através do Método do Fat Node, aqui seguimos com a utilização dos Nodes, as diferenças rondam a delimitação fixa de tamanho para a quantidade de Mods.

Um caso não abordado nesse exemplo é o cenário em que desejamos fazer alteração em um Node e este e seu antecessor ambos estão cheios. Digamos que no passo 6 do exemplo passado, o Node com valor 1 já havia sido mudado para 6 e 7 anteriormente. Da seguinte maneira:

Estado inicial:
Digamos que tendo essa estrutura a próxima operação a ser processada sendo a de remoção do Node com valor 3. De modo a realizar a operação não apenas o Node em questão deve ser divido. Mas também seu antecessor que não comporta modificação para representar a divisão.
Estado final após atualização:
Ao final do processo ambos os Nodes foram adicionados na mesma operação por esse motivo têm mesmo rótulo de versão, assim como a nova raiz criada em decorrência do processo.

Se por exemplo todos os Nodes de uma estrutura estivessem cheios de modificações e por um acaso a próxima operação visa modificar o último Node. Bem nesse caso, como no exemplo acima, o Node em que se deseja realizar a modificação seria dividido, após este processo teríamos de mudar a referência do seu antecessor para este novo Node e nesse momento este teria também de ser dividido e esse processo ocorreria por toda a estrutura até todos os Nodes tenham sido divididos em uma nova versão.

Estado inicial:
estado final após atualização:

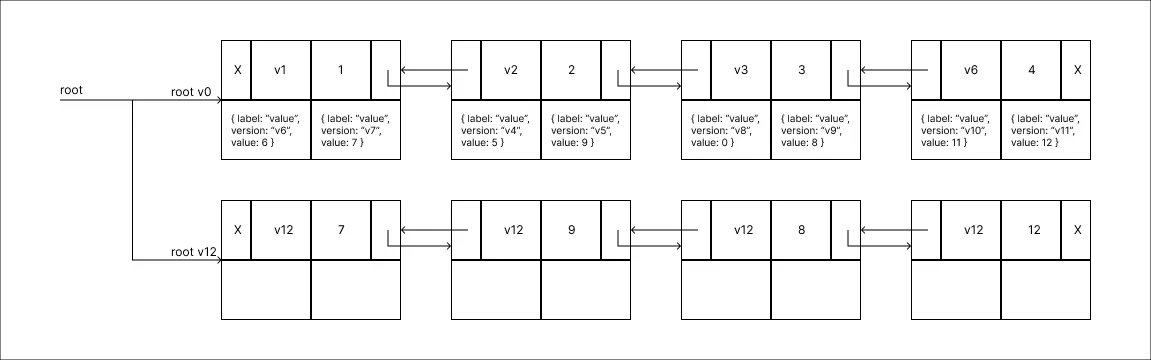
Apesar de parecer que o processo de alteração pode custar caro demais uma vez que pode disparar todos os Nodes a se dividirem, isso faz parte de uma amortização atrelada ao custo de consulta. Uma vez que com um limite de atualizações por divisão do Node e sabendo a versão a ser consultada, o processamento de busca da informação torna-se muito mais rápido, em comparação com o Método Fat Node.

Considerando um mesmo número de alterações N, enquanto no método anterior as N alterações haveriam de ser processadas, neste devido o número máximo sempre será o número estabelecido como máximo de Mods. Perceba que ao atribuir um número menor, tratando da mesma quantidade de atualizações, tendenciosamente mais divisões ocorrerão e por consequência mais Nodes serão alocados.

Conclusão

A implementação da Persistência Parcial, como visto, pode ser feita de várias formas, inegavelmente cada forma possui seus pontos fortes e fracos. Cada implementação se diferencia uma das outras principalmente quanto a utilização de recursos, tanto para escrita quanto para leitura.

Indo de soluções como a do Método das Cópias que possui uma leitura nivelada com o a implementação Efêmera, sendo separada apenas pela adição da consulta de versão, porém com uma dificuldade na escrita. Por outro lado, vimos também outro extremo o Método do Histórico que apresenta boa performance na inserção, mas deixa a desejar nas leituras. Assim como também vimos propostas que com bom equilíbrio como o caso dos métodos Fat Node e Node Splitting, que em termos de recursos são muito mais baratos que os demais.

Vale ressaltar que cada caso é um caso, assim como para as próprias Estruturas de Dados, o valor de cada método apresentado está na satisfação a uma necessidade existente. Sendo assim, apenas o próprio problema pode determinar qual a solução mais adequada para implementar Persistência Parcial.

Novamente, casos de uso para este tipo de implementação estão muito atrelados a demanda por informações do estado passado. A necessidade de retroceder algo e verificar seu estado inicial solicita ao menos uma implementação semelhante a está. E em casos mais profundos como a necessidade de ramificar a partir de qualquer ponto exigem ainda uma complexidade maior como o da Persistência Completa que pretendo abordar no futuro.

Estes foram alguns dos métodos utilizados ao longo do tempo para atingir a Persistência Parcial.

Referências

James R. Driscoll, Neil Sarnak, Daniel D. Sleator e Robert E. Tarjan - Making Data Structures Persistent - 1986